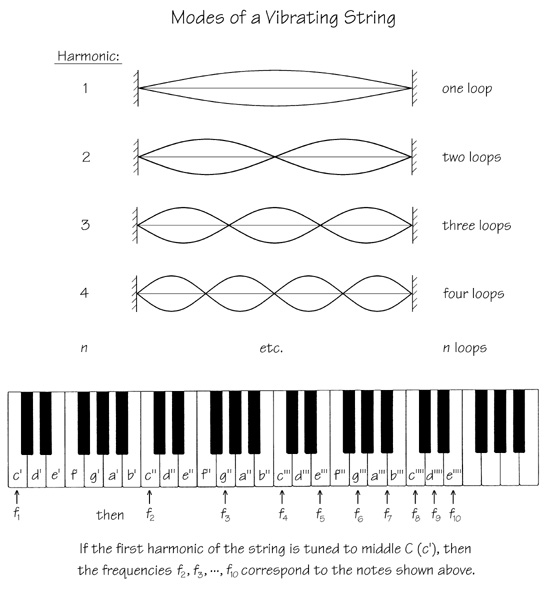
Fig. 1.2. Modes of vibration of a string fixed at both ends, along with their relative locations on the standard piano keyboard.* Each loop represents the maximum displacement above and below equilibrium (the vertical scale is exaggerated).
Harmonics
Fig. 1.2 relates each of the first ten harmonics of a vibrating string to its corresponding note in the present-day diatonic scale.

Fig. 1.2. Modes of vibration of a string fixed at both ends, along with their relative locations on the standard piano keyboard.* Each loop represents the maximum displacement above and below equilibrium (the vertical scale is exaggerated).
View an Animation of a Standing Wave. See a string, fixed at both ends, vibrating in its third harmonic, with nodes (points of zero motion) at the ends (of course) and at the one-third and two-thirds points. (Note that each point of the waveform can be percieved as vibrating up and down, or the entire waveform can be perceived as rotating in a plane perpendicular to your screen. The latter perception occurs because of the one-to-one relationship between vibratory motion and uniform circular motion.)
Hear five succesive harmonics individually and together, in sequence:
If you click this link, a new window will open. You will hear in sequence:
(1) the first harmonic (130.81 Hz): the C below middle C.
(2) the second harmonic (261.62 Hz): a C an octave above the first harmonic.
(3) Both the first and second harmonics together.
(4) the third harmonic (392.43 Hz): a G a fifth above the second harmonic.
(5) the first three harmonics together.
(6) the fourth harmonic (523.24 Hz): a C an octave above the second harmonic.
(7) the first four harmonics together.
(6) the fifth harmonic (654.05 Hz): an E a major third above the fourth harmonic.
(7) the first five harmonics together.
Note that the first, second, fourth, and eighth harmonics in Fig. 1.2. are each C’s of ascending octaves (an octave involves a 2:1 frequency ratio). Note further that (a) the third and sixth harmonics are each G’s, one octave apart, and (b) the fifth and tenth harmonics are E’s an octave apart.
Next, the notes c'' and g'' (3:2 frequency ratio) have the relationship called a fifth. The fifth is so called because G is the fifth note of the diatonic scale founded on C. A similar statement applies to the notes g''' and d''''; namely, D is the fifth note of the diatonic scale founded on G, and the ratio of the frequency of D to that of C is also 3:2.
Next, the notes c''' and e''' (5:4 frequency ratio) have the relationship called a major third. The major third is so called because E is the third note of the major diatonic scale founded on C.
Similarly, the notes c'''' and d'''' and d'''' and e'''', which theoretically involve the ratios of 9:8 and 10:9, respectively, are musical intervals called seconds because D is the second note in the key of C. And so on. The ratios 9:8 and 10:9 differ by only about 1%, which is small enough that, under most circumstances, these ratios would sound the same if played separately, in succession. However, when notes of slightly different frequency are played together, minute differences cause beats, which become quite important. Therefore, when it comes to the subject of the tuning of musical scales, we must be extremely precise. Table 1.4 relates each of the common intervals to its corresponding frequency ratio.
| Frequency Ratio | Interval | Example |
|---|---|---|
| 1:1 | unison | c'—c' |
| 2:1 | octave | c'—c'' |
| 3:2 | fifth | c''—g'' |
| 4:3 | fourth | g''—c'' |
| 5:3 | major sixth** | g''—c''' |
| 5:4 | major third | c'''—e''' |
| 6:5 | minor third | e'''—g''' |
| 7:6 | † | |
| 8:5 | minor sixth* | e'''—c''' |
| 8:7 | † | |
| 9:8 | second | c'''—d''' |
| 10:9 | second | d''''—e'''' |
**the minor sixth (8:5) is the inversion of the major third (5:4), and the major sixth (5:3) is the inversion of the minor third (6:5).
†The ratios 7:6 and 8:7 involve the seventh harmonic, which is an approximate B-flat. Consequently, intervals involving this harmonic will not be discussed.
Table 1.4. The common intervals related to their corresponding frequency ratios.
• Understand why tempered intervals beat, with audio illustrations.
*From Robert Chuckrow, Historical Tuning of Keyboard Instruments: Theory and Practice, Rising Mist Publications, Briarcliff Manor, NY, 1999, 2006, p. 5.