The Stretching of Octaves*
If you were to tune two strings exactly an octave apart using an electronic device that achieves an exact 2;1 frequency ratio, you would hear beats. This surprising result occurs for the following reason: When we tune an octave by beats, it is the second harmonic of the lower note that beats with the first harmonic of the higher note. Theoretically, the second harmonic of the lower note is twice that of the first harmonic—a perfect 2:1 ratio. In actual practice, the frequency of the second harmonic of an actual string is slightly higher than twice the frequency of its first harmonic. Thus, when the octave is tuned beatless to the second harmonic of the lower note, the octave will be stretched. The effect of higher harmonics being higher than theoretically perdicted is called inharmonicity and occurs for reasons discussed below.

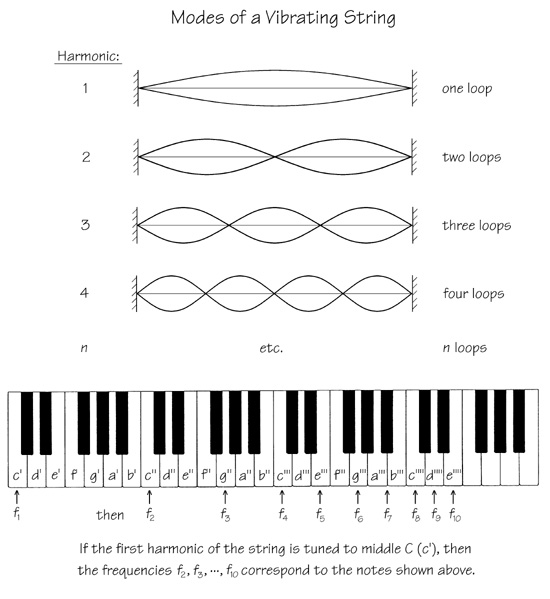
Here is the reason that the frequencies of the first and second harmonics of any string differ slightly from the theoretical 2:1 ratio: In a theoretical string, we assume that vibration can occur an infinitesimal distance from an end, and the theoretical frequency relationships are based on this assumption. But an actual string has a certain amount of stiffness that prevents any motion in a small region near each fixed end. Therefore, the effective length of an actual string is slightly less than its actual length. The explanation does not end here; there is one more consideration: The higher the harmonic, the closer an antinode (the region of maximum vibration) is to an end (see the above figure showing the harmonics of a vibrating string fixed at both ends). Because the stiffness of the string inhibits vibration near the ends of the string, the effective length of the string is reduced increasingly for each higher harmonic. Thus, the frequencies of all harmonics are higher than theoretically expected and increasingly so the higher the harmonic.
Because we want to tune a stringed instrument to have beatless octaves, we end up stretching octaves. It is, therefore, necessary that electronic tuning devices be designed to stretch octaves and other intervals to the required degree.
*From Robert Chuckrow, Historical Tuning: Theory and Practice, Rising Mist Publications, Briarcliff Manor, NY, p.12, 2006.
©Copyright 2014 by Robert Chuckrow
Read information about Robert Chuckrow’s book on historical tuning, which enables even those with very little knowledge of music theory or mathematics to achieve a historical and theoretical understanding of tuning and the ability to tune in meantone and well temperament).