Understanding and Estimating Decibels Without a Calculator or Logarithms
©1989 & 2013 Robert Chuckrow
Over the years of teaching physics and physics of sound, I developed a system by which decibels can be understood and estimated without the use of logarithms.
Decibel Scale
Weber's Law: The minimum perceptible increase in the intensity of a stimulus is proportional to the percentage increase in the stimulus.
Example: If the addition of one candle to 10 candles produces a just noticeable difference (jnd) in brightness, then the addition of 10 candles to 100 candles, or 100 candles to 1,000 candles, etc. is required to produce a jnd. In this example, the percentage increase in the stimulus is 10%.
For hearing, a jnd occurs with approximately a 25% increase in sound intensity I (I = energy per second per unit area).
Intensity-Level Scale: Since each jnd in intensity corresponds to the same multiplicative factor of 1.25 (a 25% increase), an appropriate scale to describe intensity levels should increase by equal additive amounts each time the intensity increases by the same multiplicative factor. Since it is easiest to deal with factors of 10, the simplest scale that might be tentatively proposed is:
| Intensity (Watts/m2) |
Intensity Level |
| 1 = 100 | 0 |
| 10 = 101 | 1 |
| 100 = 102 | 2 |
| 1000 = 103 | 3 |
| etc. | etc. |
Table 1.
Table 1 shows that each time the intensity increased by a factor of 10, there is a unit increase in intensity level. We see that each number on the intensity scale is the power of 10 of the intensity. Actually, the sound intensities we deal with typically range from 10–12 Watts/m2 (threshold of hearing) to 1 Watt/m2 (threshold of pain), so we prefer that the zero of the intensity level scale correspond to 10–12 Watts/m2 rather than 100.
To make this adjustment without altering the unit increase in intensity level for each factor of 10 increase in intensity, we need only divide each number in the left column by a factor of 1012, keeping the right column unchanged. Thus, we get
| Intensity (Watts/m2) |
Intensity Level (Bels) |
| 10–12 | 0 |
| 10–11 | 1 |
| 10–10 | 2 |
| 10–9 | 3 |
| etc. | etc. |
| 10–1 | 11 |
| 100 | 12 |
Table 2.
Notice that, as before, there is a unit additive increase in intensity level for each tenfold increase in intensity. Theoretically, this relationship is exactly what we want, but to be practical, we would prefer there to be a unit increase in intensity level for each jnd of intensity. The multiplicative factor in intensity would then be 1.25 rather than 10. Luckily, it turns out that ten 25% increases in intensity are about the same as our easy-to-deal-with ten-fold increase in intensity because (1.25)10 = 9.3 ≈ 10. Thus we can easily transform the above intensity level scale into a practical scale (below) by dividing it into tenths (deciBels).
| Intensity (W/m2) |
Intensity Level (Bels) |
Intensity Level (decibels) |
| 10–12 | 0 | 0 |
| 10–11 | 1 | 10 |
| 10–10 | 2 | 20 |
| 10–9 | 3 | 30 |
| etc. | etc. | etc. |
| 10–1 | 11 | 110 |
| 100 | 12 | 120 |
Table 3.
Note: Each time the sound intensity increases by a multiplicative factor of 10, there is an additive intensity level increase of 10 dB. Each time the sound intensity increases by a multiplicative factor of 1.25 there is an additive intensity level increase of approximately 1 dB.
Problems (Answers)
1. Two tones have intensities of 10–6 W/m2 and 10–3 W/m2, respectively. What is their difference in intensity level in dB?
2. What is the intensity level of each of the tones in question 1?
3. The sound intensity at a certain location is 10,000 times that at another location. By how many dB do they differ?
4. How many dB correspond to three just noticeable differences, each of a 25% increase in intensity?
Estimation of Decibel Differences Corresponding to Simple Intensity Ratios
Note: For the following estimation of decibel differences, we will use the fact that multiplicative changes in intensity produce corresponding additive increases in decibels.
First, it is obvious that an intensity ratio of one corresponds exactly to a decibel difference of zero. Moreover, we have already stated that an intensity ratio of 1.25 corresponds approximately to a decibel difference of one. Also, an intensity ratio of ten corresponds exactly to a decibel difference of ten. Summarizing:
| Intensity Ratio | Decibel Difference |
| 1 | 0 |
| 1.25 | 1 |
| 10 | 10 |
Note that (1.25) (1.25) = (5/4)2 = 25/16 = 1.56 ≈ 1.5. Therefore, an increase of 50% (a factor of 1.5) in intensity corresponds to an approximate increase of 2 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 1.5 | 2 |
Next, (1.25) (1.25) (1.25) = (5/4)3 = 125/64 = 1.95 ≈ 2. Therefore, an increase of 100% (a factor of 2) in intensity corresponds to an approximate increase of 3 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 2 | 3 |
Next, an intensity ratio of three is a 50% increase over an intensity ratio of two; namely, 3 = 2 (1.5). Thus, a factor of 3 increase in intensity corresponds to an approximate increase of 3 dB + 2 dB = 5 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 3 | 5 |
Moreover, an intensity ratio of four is twice an intensity ratio of two; namely, 4 = 2 × 2. Thus, a factor of 4 increase in intensity corresponds to an approximate increase of 3 dB + 3 dB = 6 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 4 | 6 |
An intensity ratio of 5 is 1.25 times an intensity ratio of four; namely, 5 = 4 × 1.25. Thus, a factor of 5 increase in intensity corresponds to an approximate increase of 6 dB + 1 dB = 7 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 5 | 7 |
An intensity ratio of 6 is twice an intensity ratio of three; namely, 6 = 2 × 3. Thus, a factor of 6 increase in intensity corresponds to an approximate increase of 3 dB + 5 dB = 8 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 6 | 8 |
An intensity ratio of 8 is twice an intensity ratio of four; namely, 8 = 2 × 4. Thus, a factor of 8 increase in intensity corresponds to an approximate increase of 3 dB + 6 dB = 9 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 8 | 9 |
An intensity ratio of 7 does not involve any multiple of integers. However, we have just found that intensity ratios of 6 and 8 correspond to decibel differences of 8 dB and 9 dB, respectively. Therefore, we can estimate that an intensity ratio of 7 approximately corresponds to 8.5 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 7 | 8.5 |
Similarly, we can estimate that an intensity ratio of 9 approximately corresponds to 9.5 dB. Summarizing:
| Intensity Ratio | Decibel Difference |
| 9 | 9.5 |
All of the above results are summarized in the following table:
| Intensity Ratio | Decibel Difference |
| 1 | 0 |
| 1.25 | 1 |
| 1.5 | 2 |
| 2 | 3 |
| 3 | 5 |
| 4 | 6 |
| 5 | 7 |
| 6 | 8 |
| 7 | 8.5 |
| 8 | 9 |
| 9 | 9.5 |
| 10 | 10 |
Table 4.
We can also work backwards. For example, a dB difference of 4 can be broken down into 4 = 3 + 1, corresponding to intensity ratios of 2 and 1.25. Thus 4 dB corresponds to an intensity ratio of 2 × 1.25 = 2.5, as expected from interpolating intensity ratios in Table 4 corresponding to 3 dB and 4 dB.
Estimation of Decibel Differences Corresponding to Intensity Ratios larger than 10
An intensity ratio of, say, 20 can be thought of as the product of 10 and 2. Thus the corresponding decibel difference is 10 + 3 =13 dB. Similarly, an intensity ratio of 30 can be thought of as the product of 10 and 3. Thus the corresponding decibel difference is 10 + 5 =15 dB. Finally, an intensity ratio of 40 can be thought of as the product of 10, 2, and 2. Thus the corresponding decibel difference is 10 + 3 + 3 = 16 dB. And so on.
The above results are summarized in the following table:
| Intensity Ratio | Decibel Difference |
| 20 | 13 |
| 30 | 15 |
| 40 | 16 |
| 50 | 17 |
| 60 | 18 |
| 70 | 18.5 |
| 80 | 19 |
| 90 | 19.5 |
| 100 | 20 |
Table 5.
Problems (Answers)
5. Estimate the decibel difference corresponding to the following intensity ratios: a) 2, b) 4, c) 5, d) 8, e) 8 × 103.
6. Estimate the approximate intensity ratio corresponding to each of the following decibel differences: a) 1, b) 2, c) 3, d) 4, e) 5, f) 6, g) 41, h) 52, i) 63, j) 57.
Variation of Intensity Level with Distance from the Source
When a source radiates sound energy uniformly in all directions, the intensity varies inversely with the square of the distance (I ∝ 1/r2). The reason for this relationship is that, at twice a given distance from the source, all the energy must cross a surface area four times as large (Asphere = 4πr2). Since the intensity level drops by 3 dB for every halving of the intensity, a doubling of the distance (a quartering of the intensity) corresponds to a 6-dB drop. The following chart summarizes the concepts:
| Distance From Source (ft) |
Factor by which Distance is Multiplied |
Factor by which I is Multiplied |
Amount by which dB Level is Changed |
Intensity Level (dB) |
| 1 | 1 | 1 | 0 dB | 100 |
| 2 | 2 | 1/22 = 1/4 | -6 | 94 |
| 4 | 4 | 1/42 = 1/16 | –12 | 88 |
| 10 | 10 | 1/102 = 1/100 | –20 | 80 |
| 20 | 20 | 1/202 = 1/400 | –(6 + 20) = –26 | 74 |
| 40 | 40 | 1/402 = 1/1600 | –(12 + 20) = –32 | 68 |
| 100 | 100 | 1/1002 = 10-4 | –40 | 60 |
| 200 | 200 | 1/2002 = (1/4) × 10–4 | –(6 + 40) = –46 | 54 |
| 400 | 400 | 1/4002 = (1/16) × 10–4 | –(12 + 20) = –52 | 48 |
| 1,000 | 1,000 | 1/1,0002 = 10–6 | –60 | 40 |
| 2,000 | 2,000 | 1/2,0002 = (1/4) × 10–6 | –(6 + 60) = –66 | 34 |
| 1/2 | 1/2 | 22 = 4 | +6 | 106 |
| etc. | etc. |
Decibel levels at different distances from a source, radiating uniformly in all directions, producing a 100-dB intensity level 1 ft away.
Note: Each doubling of the distance from the source quarters the intensity and produces a drop in intensity level of 6 dB.
Problems (Answers)
7. The intensity level at a distance 1 ft from a siren radiating in all directions is 80 dB. What is the intensity level at each of the following distances from the siren? a) 2 ft, b) 10 ft, c) 20 ft, d) 100 ft.
8. If two sirens of the type in problem 9 are radiating together, what is the intensity level of the two at a distance 1 ft away from both? Hint: The intensities simply add.
9. How many sirens sounding together have an intensity level 10 ft away that is 6 dB lower than that 1 ft away from one such siren?
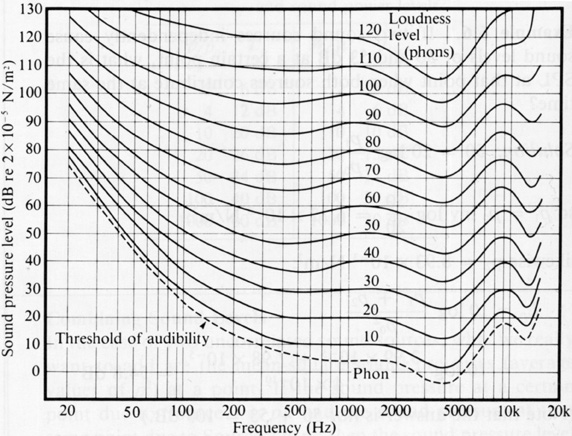
Equal-Loudness Curves
The human auditory system has an inherent non-uniform response to tones of the same intensity but of different frequency. Moreover, this non-uniformity changes with intensity. Therefore, we introduce a new concept termed loudness level, which is measured in phons.
Definition: The loudness level (in phons) of a tone is the intensity level of a 1,000-Hz tone that sounds equally loud.
Note: It follows from the above definition that the loudness level (phons) and intensity level (dB) of a 1000-Hz tone of any intensity are the same.

The above figure shows equal-loudness curves,* which are used for the following problems:
Problems (Answers)
10. Two tones, each of 50 Hz, have intensity levels of 50 dB and 120 dB, respectively. What is the loudness level of each in phons? (Refer to the equal-loudness curves above.)
11. Three tones of 50 Hz, 1,000 Hz, and 5,000 Hz each have a loudness level of 60 phons. What is the intensity level in dB of each?
12. A 100-Hz tone of intensity level 50 dB is about as loud as a 1000-Hz tone of intensity level 40 dB. (You can see this relationship by examining the equal-loudness curves above). What is the ratio of the intensity of the 100-Hz tone to that of the 1,000-Hz tone?
13. What is the intensity level of a 50-Hz tone that sounds as loud as a 5,000-Hz tone of intensity level 40 dB?
Treatment of Decibels Using Logarithms
The following treatment using logaritms is shown for those that desire a more-rigorous treatment.
Consider the following relationship:
| y = 10x | Eq. (1) |
Substituting successive integers for x, we get the following correspondence:
| x | y |
| 0 | 1 |
| 1 | 10 |
| 2 | 100 |
| 3 | 1,000 |
| etc. | etc. |
Inspection of the above table reveals a relationship similar to that between decibels and intensity ratios. Namely, if y were the intensity ratio, then 10x would be the decibel difference ΔdB. Stated mathematically:
| I2/I1 = 10ΔdB/10 | Eq. (2) |
For example, if two sounds differ in intensity level by 20 dB, then, substituting into Eqn. 2, we get
I2/I1 = 1020/10
I2/I1 = 102 = 100.
Whereas Eq. 2 can be used for finding the intensity ratio if the decibel difference is known, we are more often interested in finding the decibel difference when given the intensity ratio.
It is known that the inversion of Eq. 1 is:
x = Log10y
Thus, the following formula for the decibel difference ΔdB of two intensities I2 and I1 applies:
| ΔdB = 10 log10 (I2/I1) | Eq. (3) |
For example, if I2/I1 = 1.25 (a 25% increase), we get a decibel difference of
ΔdB = 10 log10 1.25 = 10(0.0969) = 0.969 ≈ 1 dB.
Or, if I2/I1 = 1,000, we get a decibel difference of
ΔdB = 10 log10 1,000 = 10 (3) = 30 dB.
Note that if I2/I1 = 1, Eq. 3 gives a decibel difference of zero, as expected.
Problems (Answers)
14. Use Eq. 2 to calculate the intensity ratio corresponding to each of the following decibel differences: a) 1, b) 2, c) 3, d) 4, e) 5, f) 6.
15. Use Eq. 3 to calculate the decibel difference corresponding to the following intensity ratios: a) 2, b) 4, c) 5, d) 8, e) 8 × 103.
16. Use Eq. 3 to calculate the decibel levels in Table 4. Then check the estimated values for accuracy.
Additional Problems (Answers)
17. Estimate the intensity level in dB of the threshold of audibility at each of the following frequencies: a) 30 Hz, b) 100 Hz, c) 1,000 Hz, d) 5,000 Hz.
18. Estimate the decibel difference corresponding to each of the following intensity ratios: a) 1.25, b) 2, c) 4, d) 5, e) 8, f) 10, g) 20, h) 100, i) 125, j) 200, k) 1,000, l) 1,000,000.
19. Estimate the intensity ratio corresponding to each of the following decibel differences: a) 1 dB, b) 3 dB, c) 6 dB, d) 9 dB, e) 10 dB, f) 11 dB, g) 13 dB, h) 16 dB, i) 30 dB, j) 50 dB, k) 53 dB.
20. A sound source produces an intensity of 10–9 W/m2 at 10 ft away. Estimate the intensity at each of the following distances from the source: a) 20 ft, b) 30 ft, c) 40 ft, d) 50 ft, e) 100 ft.
21. A sound source produces 40 dB at 10 ft away. Estimate the decibel level at each of the following distances from the source: a) 20 ft, b) 30 ft, c) 40 ft, d) 50 ft, e) 100 ft.
22. At what decibel level is a 100-Hz sound as loud as a 1,000-Hz sound at 40 dB?
23. At what decibel level is a 30-Hz sound as loud as a 3,000-Hz sound at 50 dB?
©1989 and 2013 Robert Chuckrow, revised 5/24/13